Recall that the Riemann tensor is
In a local inertial frame we have 
,
so in this frame
Now
so
since 
i.e the first derivative of the metric
vanishes in a local inertial frame. Hence
Using the fact that partial derivatives always commute so that
, we get
in a local inertial frame. Lowering the index 
with the metric
we get
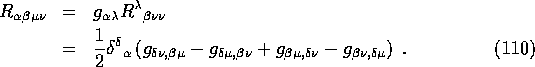
So in a local inertial frame the result is
We can use this result to discover what the symmetries of
are. It is easy to show from the above
result that
and
Thus is antisymmetric on the final pair
and second pair of indices, and symmetric on exchange of the
two pairs.
Since these last two equations are valid tensor equations, although they were derived in a local inertial frame, they are valid in all coordinate systems.
We can use these two identities to reduce the number of independent
components of from 256 to just
20 .
A flat manifold is one which has a global definition of parallelism: i.e. a vector can be moved around parallel to itself on an arbitrary curve and will return to its starting point unchanged. This clearly means that
i.e. the manifold is flat [ Assignment 6.5: try a cylinder! ].
An important use of the curvature tensor comes when we examine the
consequences of taking two covariant derivatives of a vector field
:
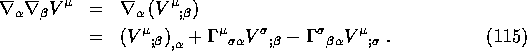
As usual we can simplify things by working in a local inertial frame. So in this frame we get
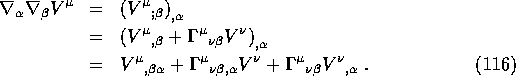
The third term of this is zero in a local inertial frame, so we obtain
Consider the same formula with the and 
interchanged:
If we subtract these we get the commutator of the covariant derivative
operators 
and 
:
The terms involving the second derivatives of 
drop
out because 
[ partial
derivatives commute ].
Since in a local inertial frame the Riemann tensor takes the form
we get
This is closely related to our original derivation of the Riemann
tensor from parallel transport around loops, because the parallel
transport problem can be thought of as computing, first the change of
in one direction, and then in another, followed by
subtracting changes in the reverse order.